Skip to main content

Normalization

Notion Notes

What is a good relation design (Well-Structured Relation)?#

We have seen how to create a new relation from a given schema.

We know that the following rules must apply to relations:

  1. Entity Integrity: For each tuple in a relation attributes that belong to the primary key must be non-null
  2. Referential Integrity: All foreign key attribute values in a relation must be either null or correspond to a primary key value
  3. Duplication of tuples in a relation is not allowed.
  4. Next, we look at: - Normalization

Basically, a well-structured relation is a relation that contains minimal data redundancy and allows users to insert, delete, and update rows without causing data inconsistencies. Its goal is to avoid (minimize) anomalies:

  • Insertion Anomaly: adding new rows forces user to create duplicate data
  • Deletion Anomaly: deleting a row may cause loss of other data representing completely different facts
  • Modification Anomaly: changing data in a row forces changes to other rows because of duplication

General rule of thumb: a table should not pertain to more than one entity type

Normalization#

Normalization（规范化表格）is a technique used to organize the data in a database.

  • Normalization consists of a set of rules that all relations must follow for a database(DB) to be well structured.
  • These rules are presented as sets of restrictions called NORMAL FORMS

Normalization is the process of creating a DB that complies with these restrictions. We do that by normalizing each of the relations.

  • Normal forms:
    • 1NF (First Normal Form)
    • 2NF (Second Normal Form)
    • 3NF (Third Normal Form)
    • 4NF, 5NF, 6NF...... It's not always a good idea to normalize beyond 3NF.

Applying these rules removes undesirable properties from a DB, including the removal of data anomalies: UPDATE ANOMALY, INSERTION ANOMALY, DELETION ANOMAL

Anormalies | Example: Relation TA#

dsd

The relation TA is not normalized. Why does this matter?

  1. What are the CANDIDATE KEYS of TA?

    • {TA_ID, TA_DEPT}

  2. What is the PRIMARY KEY of TA?

    • {TA_ID, TA_DEPT}

  3. UPDATE ANOMALY

  • Ann belongs to two departments
  • If Ann's address changes, we will need to update two tuples, to avoid ambiguity

  1. INSERTION ANOMALY

  • Suppose a new TA has been appointed but does not yet know which department they will work in.
  • We cannot put a NULL to TA_DEPT because primary key value cannot be NULL.
  • We would not be able to INSERT the data into the relation. —> INSERTION ANOMALY

  1. DELETION ANOMALY

  • Suppose the BIOLOGY department is closed down
  • Deleting tuples with attribute value BIOLOGY in TA_DEPT would delete the information about Bob — we do not want to remove Bob's TA_ID, TA_ADDRESS, and other information — thus a DELETION ANOMALY

How do we resolve or avoid anomalies?

  • To resolve or avoid anomalies, we need to normalize relations
  • We will continue the above example later in the lecture, after we have discussed 1NF and 2NF.

Normal Forms#

Normalization consists of a set of rules that all relations must follow for a database(DB) to be well structured. These rules are presented as sets of restrictions called NORMAL FORMS.

First Normal Form（1NF)#

Each attribute name must consist of a single item.

Each attribute value must represent a single fact.

Example:

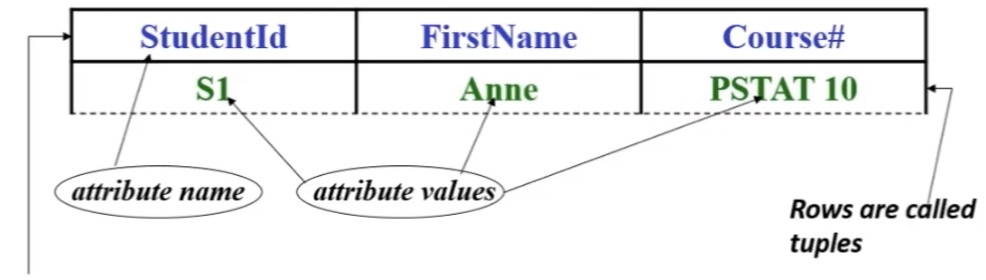
dqsiF2MuIDPhEVS

A single fact:

Anne is a single fact regarding FirstName; PSTAT 10 is a single fact regarding Course#......

Example: Relation COURSE_CONTENT#

A DB design team has been working on the relationships between each COURSE and its SYLLABUS in the Statistics Department. They suggest the following relation.

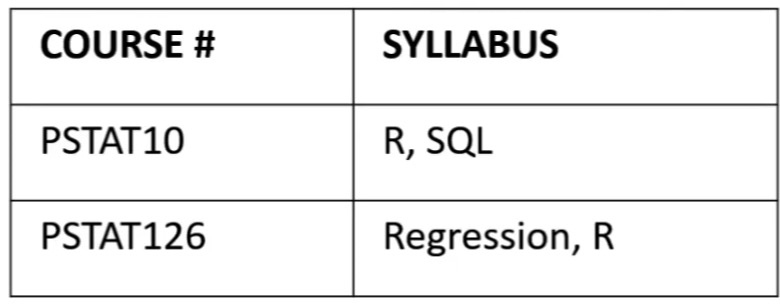
course

COURSE #: PSTAT10, PSTAT126 —— OK

SYLLABUS: R,SQL Regression, R —— two separate facts

Thus COURSE_CONTENT Not in 1NE

Example: Decomposing A Relation Into First Normal Form(1NF)#

1NF

R, SQL for PSTAT10 become separate tuples.

So COURSE_CONTENT2 is in 1NF

A new example:

course

It violates both rules for 1NF

Decompose Into 1NF#

Example: COURSE_CONTENT_3#

course_content_3

Because there 2 tuple values in COURSE_CONTENT

We can decompose it:

course_content_3
course_content_4

Second Normal Form (2NF)#

A relation is in 2NF if both of the following conditions hold:

  • It is in 1NF (first normal form).
  • No non-prime attribute is functionally dependent on a proper subset of any candidate key.

Non-prime attribute#

An attribute that is not part of any candidate key is a NON-PRIME ATTRIBUTE.

✨ Functionally dependent#

If a set of attributes A of a relation uniquely identifies a set of attributes B of the same relation, then B is FUNCTIONALLY DEPENDENT on A. Written: A-->B (just one long arrow)


In other words, the value of one attribute (the determinant) determines the value of another attribute.

– A-->B reads “Attribute B is functionally dependent on A” – A-->B means if two rows have same value of A they necessarily have same value of B – FDs are determined by semantics: You can’t say that a FD exists just by looking at data. But can say whether it does not exist by looking at data.


Proper subset#

A proper subset of a set A is a subset of A that is not equal to A.


Example: Functional Dependencies (FD's)#

If a set of attributes A of are relation uniquely identifies a set of attributes B of the same relation, then B is FUNCTIONALLY DEPENDENT on A. Written:A--->B

Schema: STUDENT (ID, NAME, ADDRESS)

{ID} uniquely identifies the following sets of attributes {NAME}, {ADDRESS}, {NAME, ADDRESS}

  • If {ID} uniquely identifies {NAME, ADDRESS}, then it also uniquely identifies {NAME} and {ADDRESS}.

NAME and ADDRESS are both FUNCTIONALLY DEPENDENT on ID. Written:

  • {ID}--->{NAME}
  • {ID}--->{ADDRESS}
  • {ID}--->{NAME, ADDRESS}

(Not required to use {}, just be absolutely clear about what you're meaning)

Theory of relational database replies on advanced set theory. It's mathematically precise and consistent. If you do more work in database, you will need to understand quite a lot of set theory before you can continue.

Continued:

  • ID--->{NAME} (read: NAME is functionally dependent on ID)
  • ID--->{ADDRESS}
  • ID--->{NAME, ADDRESS}

ID--->{NAME} can therefore also be read: ID functionally determines NAME

  • You should be familiar with both of these terms with both functionally dependent and functionally determines.
  • MEANING:
    • For any given ID, there can only be one name. Similarly, for address.
  • However, it would be incorrect to write NAME-->{ID}
    • MEANING:
      • For any given NAME, there can only be one ID —— not the case
      • NAME functionally determines ID and ID is functionally determined by NAME

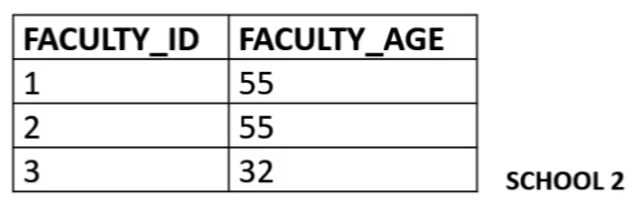
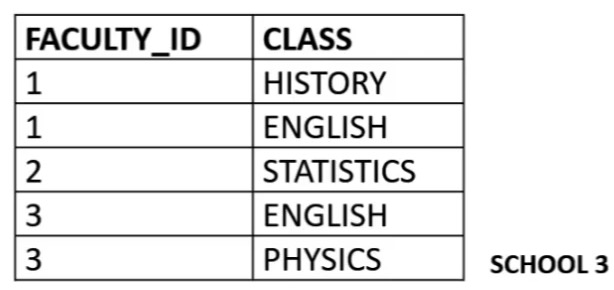
Example: 2NF Relation SCHOOL#

SCHOOL

  1. Is the relation SCHOOL in 1NF?

  2. Are there any non-prime attributes that are functionally dependent on a proper subset of any candidate key?

    If so, the relation is not in 2NF.

    • Candidate key: {FACULTY_ID, CLASS}

    • Proper subsets of candidate keys: {FACULTY_ID},{CLASS}

    • Non-Prime attributes: {FACULTY, AGE} (An attribute that is not part of any candidate key is a non-prime attribute)

    • Identify Functional Dependencies (FD's) associated with non-prime attributes.

      Does FACULTY_ID---> FACULTY_AGE hold? YES.

    • Non-prime attribute FACULTY_AGE is dependent on FACULY_ID which is a proper subset of the candidate key.

Therefore, the relation SCHOOL is not in 2NF.

Why does whether the relation is 2NF or not matters?#

  • Because there are possibility of Update anomalies, Insertion anomalies and Deletion anomalies.

  • Try to think of some possible anomalies.

Summary of examples so far#

  • Is the SCHOOL below in 1NF? —— YES

  • Candidate key: {FACULTY_ID, CLASS} and hence Primary Key Non-Prime attributes: FACULTY_AGE

  • Relation not in 2NF

  • The non-prime attribute FACULTY_AGE is functionally dependent on FACULTY_ID.

    This violates 2NF which requires that:

    No non-prime attribute is functionally dependent on a proper subset of any candidate key.

Decompose into 2NF#

按照“主键的值可以确定其他列的值”原则来分表

Steps:

  1. When there is an FD, X-->Y on part of the candidate key(X is part of candidate key), form a new relation with X as primary key and with all the attributes determined by X.
  2. Form a new relation defined on the attributes of the candidate keys of the original relation and include all attributes that are not functionally determined by only part of the key.

Example(continued):

  • The candidate key is: {FACULTY_ID, CLASS}
    ta

Applying the steps to the SCHOOL relation

  1. STEP 1

    • FACULTYID ---> FACULTY_AGE (READ: FACULTYID functionally determines FACULTY_AGE)
    • Form a new relation with FACULTY_ID as primary key and FACULTY_AGE as attribute
      SCHOOL2

  1. STEP 2

    • Form a new relation defined on the attributes of the key of the original relation. New relation has FACULTY_ID, CLASS as attributes./>
    • FACULTY_AGE is determined by only part of the key, so is not included.
      SCHOOL3

Example: Relation TA Continued#

SCHOOL

Normalize the TA relation to comply with 2NF#

  1. TA is in 1NF

  2. Candidate key: {TA_ID, TA_DEPT}

  3. Non-prime attributes: {TA_NAME, TA_ADDRESS}

  4. Functional dependencies:

    1. TA_ID--->{TA_NAME, TA_ADDRESS}
    2. TA_ID--->{TA_NAME}
    3. TA_ID--->{TA_ADDRESS}

  5. Non-prime attributes functionally dependent on proper subset of candidate key, so TA not in 2NF

  6. So we need to decompose it into 2NF:

    1. Step 1: When there is an FD, X-->Y on part of the candidate key, form a new relation with X as primary key and with all the attributes determined by X.

      • FD: TA_ID--->{TA_NAME} and TA_ID--->{TA_ADDRESS}
      • Candidate keys: {TA_ID, TA_DEPT}
      • Form a new relation with TA_ID as primary key and TA_NAME and TA_ADDRESS as attributes
      TA2

    Duplicate tuples removed because of primary key in new relation

    1. Step 2: Form a new relation defined on the attributes of the candidate keys of the original relation and include all attributes that are not functionally determined by only part of the key.

      • Candidate keys: {TA_ID, TA_DEPT}
      • {TA_NAME} and {TA_ADDRESS} are functionally determined by TA_ID, which is part of the key —— so are not included in the new relation attributes
      • New relation attributes: {TA_ID}, {TA_DEPT}
      ta3

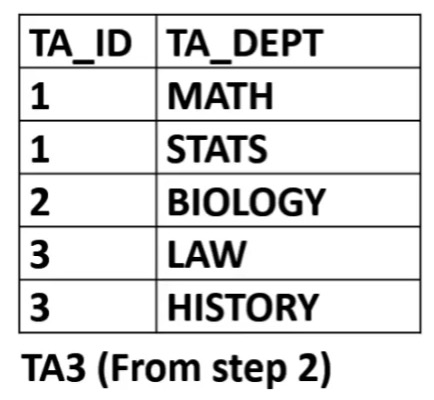
UPDATE ANOMALY#

Ann belongs to two departments. If Ann's address changes, we will need to update TWO tuples to avoid ambiguity.

Ann's address might be updated in MATH but not in STATS; an inconsistency.

Have we resolved the update anomaly?

Yes. We only need update ONE tuple. —— update the first tuple in TA2

INSERT ANOMALY#

Suppose a new TA has been appointed but does not yet know which department they will work in.

Have we resolve the INSERT anomaly?

Yes. We can record the new TA's details without having to specify their department.

DELETE ANOMALY#

Suppose the BIOLOGY department is closed down.

Deleting tuples with attribute value BIOLOGY in TA_DEPT would delete the information about Bob.

Have we resolve the DELETE anomaly?

Yes. We can delete biology department without deleting Bob's information.

3NF Lecture Notes

3NF quickly beyonds the scope of PSTAT10. All we need to know is the content mentioned in the powerpoint slides.

Third Normal 3NF#

A relation is in 3NF if both of the following conditions hold:

  1. the relation is in 2NF.
  2. there are no TRANSITIVE FUNCTIONAL DEPENDENCIES of NON-PRIME ATTRIBUTES on the primary key.

Transitive Functional Dependencies#

If A--->B and B--->C are two Functional Dependencies, then A--->C is a TRANSITIVE FUNCTIONAL DEPENDENCY.

Recall:

  • If a set of attributes A of a relation uniquely identifies a set of attributes B of the same relation, then B is FUNCTIONALLY DEPENDENT on A. Written: A ---> B
  • An attribute that is not part of any candidate key is a NON-PRIME ATTRIBUTE.

A simple example of 3NF#

Consider the following relation schema: Student_Address (STUDENT_ID, STUDENT_NAME, ZIP, STATE, CITY)

It's always important to state your assumptions

Assumptions: Each student has a unique STUDENT_ID and only one address, denoted by ZIP, STATE, CITY

Review for these concepts:

  • Super-keys: {STUDENT_ID}, {STUDENT_ID, STUDENT_NAME} and so on…

  • Candidate keys: {STUDENT_ID}

  • Primary key: {STUDENT_ID}

  • Non-prime attributes: {STUDENT_NAME, ZIP, STATE, CITY}

2NF will hold Relation is in 1NF and no non-prime attribute is functionally dependent on a proper subset of any candidate key.

3NF will hold if there are no TRANSITIVE FUNCTIONAL DEPENDENCIES of NON-PRIME ATTRIBUTES on the primary key.

ZIP is functionally dependent on STUDENT_ID.

STATE and CITY is functionally dependent on ZIP.

Thus,

  • STUDENT_ID —> ZIP
  • ZIP —> {STATE, CITY}

If A —> B and B —> C are two FDs, then A —> C is a transitive functional dependency.

{STATE, CITY} is transitively functionally dependent on STUDENT_ID, STUDENT_ID —> {STATE, CITY}

STATE and CITY are non-prime attributes. STUDENT_ID is the primary key.

Thus, the relation STUDENT_ADDRESS violates third formal form requirements, not in 3NF.

Decompose into 3NF#

Example continued#

  • Student_Address (STUDENT_ID, STUDENT_NAME, ZIP, STATE, CITY)

  • STUDENT_ID —> ZIP functional dependency

  • ZIP —> {STATE, CITY} functional dependency

  • STUDENT_ID —> {STATE, CITY} transitive functional dependency

In order to conform with 3NF, we need to remove that transitive functional dependency.

Form a new relation that includes all attributes in the schema except those that were transitively determined.

New relation schema: SA2 (STUDENT_ID, STUDENT_NAME, ZIP) (not include STATE, CITY)

This leaves us with attributes STATE and CITY.

→ Form a new relation defined on these attributes with ZIP as primary key, since ZIP —> {STATE, CITY}

New relation schema: SA3 (ZIP, STATE, CITY)

Edit this page